그래프

그래프는 연결되어 있는 원소간의 관계를 정의한 것을 그래프라고 한다.

그래프

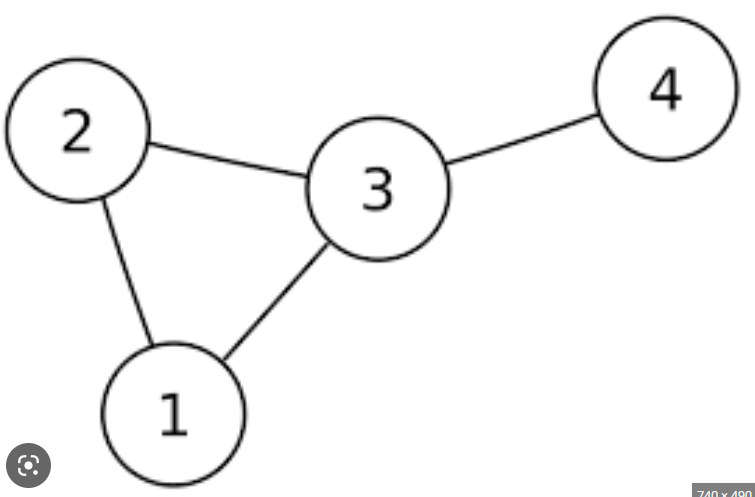
그래프는 양방향 그래프, 단방향 그래프가 있는데 양방향 그래프는 위의 그림과 같이 방향이 표시 되어 있지 않지만 둘 다 연결되어 있는 것이다.

단방향 그래프는 방향이 존재한다.

단방향 그래프

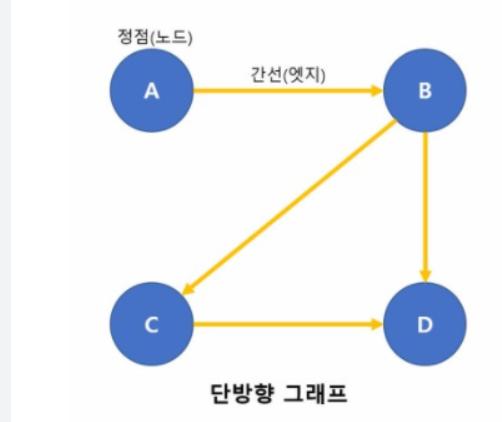
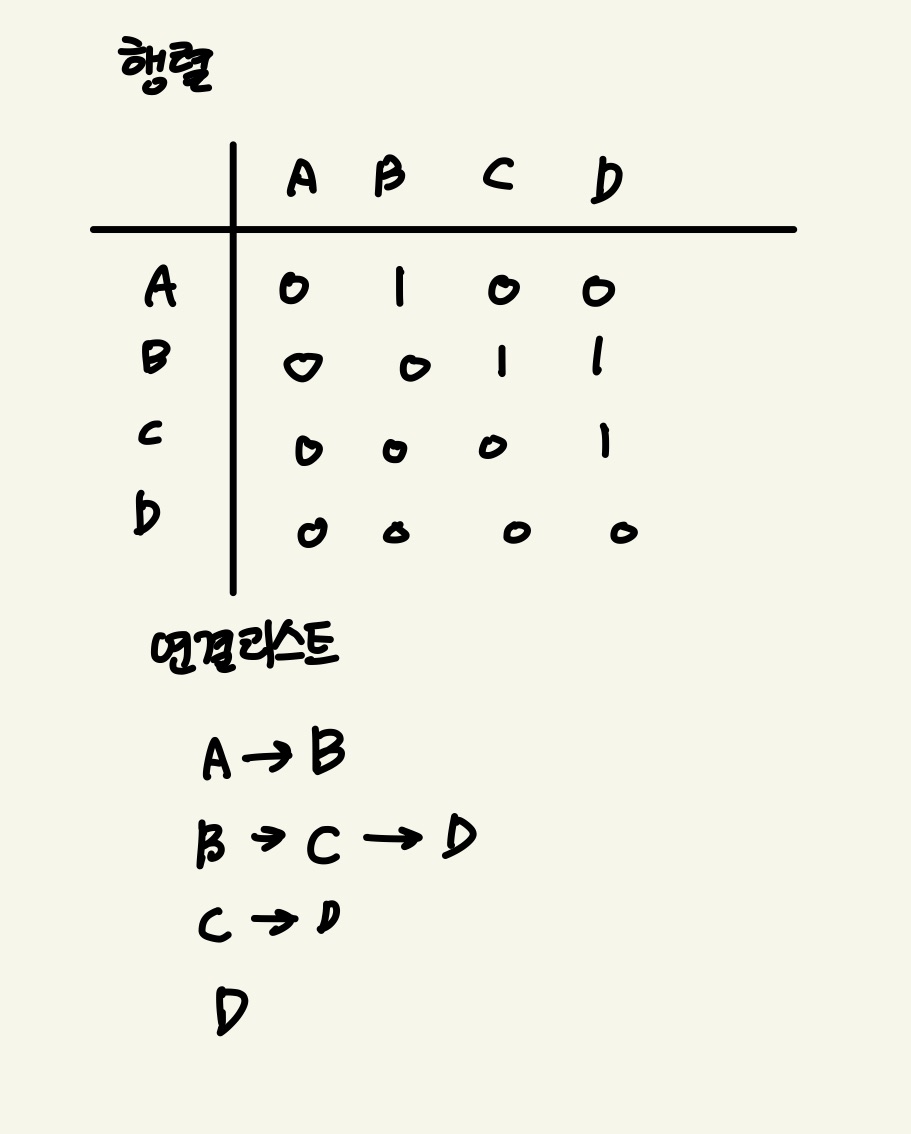
이것에 대한 표현은 연결리스트나 행렬로 할 수 있다.

연결리스트, 행렬

그래프의 탐색에는 두 가지 방법이 있다.

DFS/ BFS

 

DFS

 

DFS는 Depth first search 로 깊이 우선 탐색이라고 한다.

노드에 방문하고 해당 노드에 연결된 첫번째 노드부터 쭉 따라 들어가면서 탐색 하는 것이다.

DFS는 스택으로 구현을 하게 된다.

DFS

연결리스트 DFS

// not yet

인접행렬 DFS

3 x 3행렬로 해봤을 때

3*3 인접행렬

방문결과

dfs 인접행렬 코드

void dfs(int** matrix, int* visited, int vertex)
{
    int i = 0, j = 0;
    for (int current_vert = 0; current_vert < col; current_vert++) {
        if (matrix[vertex][current_vert] == 1 && !visited[current_vert]) {
            visited[current_vert] = 1;
            std::cout << current_vert << " ";
            dfs(matrix, visited, current_vert);
        }
    }
}

방문했던 곳을 다시 방문하지 않기 위해 visited 배열을 vertex 개수만큼 하나 만들어서 방문할 때마다 표시해준다.

해당 구현 코드

#include <stdio.h>
#include <stdlib.h>
#include <iostream>

void dfs(int** matrix, int* visited, int vertex);
void insert_graph_node(int** matrix, int start, int end);
int** make_mat();
void init_mat(int** matrix);
void free_mat(int** matrix);
void print_mat(int** matrix);

int row = 0;
int col = 0;

int main(void)
{
    int i = 0;
    std::cin >> row >> col;
    int* visited = (int*)malloc(sizeof(int) * row);
    for (int i = 0; i < row; i++) {
        visited[i] = 0;
    }

    int** matrix = make_mat();
    init_mat(matrix);

    insert_graph_node(matrix, 1, 2);
    insert_graph_node(matrix, 1, 0);
    insert_graph_node(matrix, 2, 1);
    insert_graph_node(matrix, 0, 2);
    insert_graph_node(matrix, 0, 1);


    print_mat(matrix);

    printf("\n");
    dfs(matrix, visited, 0); // vertex는 배열 인덱스 기준

    free(visited);
    free_mat(matrix);
}
int** make_mat()
{
    int** matrix = (int**)malloc(sizeof(int*) * row);
    for (int i = 0; i < row; i++) {
        matrix[i] = (int*)malloc(sizeof(int) * col);
    }
    return matrix;
}
void init_mat(int** matrix)
{
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            matrix[i][j] = 0;
        }
    }
}
void free_mat(int** matrix)
{
    for (int i = 0; i < row; i++) {
        free(matrix[i]);
    }
    free(matrix);
}
void insert_graph_node(int** matrix, int start, int end)
{
    if ((start < 0 || end < 0) || (start >= row || end >= col)) {
        fprintf(stderr, "Wrong access, index overrun");
        std::cout << std::endl;
        return;
    }
    else {
        matrix[start][end] = 1;
    }
}
void print_mat(int** matrix)
{
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            std::cout << matrix[i][j]<<" ";
        }
        std::cout << std::endl;
    }
}

BFS

// not yet

 

가중치 그래프

그래프에서는 위의 그림들처럼 노드별로 연결되어 있는 선이 있는데 해당 선마다의 가중치를 줄 수 있다.

즉 그 선을 지나기 위해서 필요한 cost (비용)을 설정해줄 수 있다.

가중치 그래프